Hi! My name is Alex and I am a researcher at OpenAI working on image generation.
Until recently, I was the co-founder and CTO at Luma AI, where I worked on generative models, especially
dream-machine, a frontier video generative model, and genie, a text-to-3d model.
Previously, I graduated from UC Berkeley, where I majored in CS and applied math and worked with Prof. Angjoo Kanazawa in BAIR. While at Berkeley, I also interned at Google and Adobe, helped search for aliens at SETI, particiated in programming competitions, and released various open source projects on Github, among other things. Before Berkeley, I lived in Vancouver, Canada for many years.
News
- March 2025: Joined OpenAI imagegen team.
- August 2024: Luma released Dream Machine 1.5
- June 2024: Invited talk at CVPR 3D generation workshop AI3DG on Dream Machine and connecting it to our previous 3D work. Slides are available here.
- June 2024: Luma released Dream Machine, our first video model
- November 2023: Luma released Genie, a 3D foundation model
- August 2023: Co-organized and presented at Neural Fields course at SIGGRAPH 2023
- June 2023: Invited talk at CVPR XRNeRF workshop with Amit Jain
Foundation models and research works
Dream Machine
A generative video model that generates 120 frames of high-fidelity video from a image or text prompt, in under 120 seconds. Built on a transformer architecture and trained directly on videos, dream machine shows a promising level of 3D and physical consistency. We followed this with advanced control capabilities such as keyframe-control and looping.
Genie: Text to 3D foundation model
A foundation model for generating 3D assets from a text prompt within 10 seconds, along with a refine process to achieve higher quality models.

Plenoxels: Radiance Fields Without Neural Networks
We introduce Plenoxels (plenoptic voxels), a system for photorealistic view synthesis. Plenoxels represent a scene as a sparse 3D grid with spherical harmonics. This representation can be optimized from calibrated images via gradient methods and regularization without any neural components. On standard, benchmark tasks, Plenoxels are optimized two orders of magnitude faster than Neural Radiance Fields with no loss in visual quality.
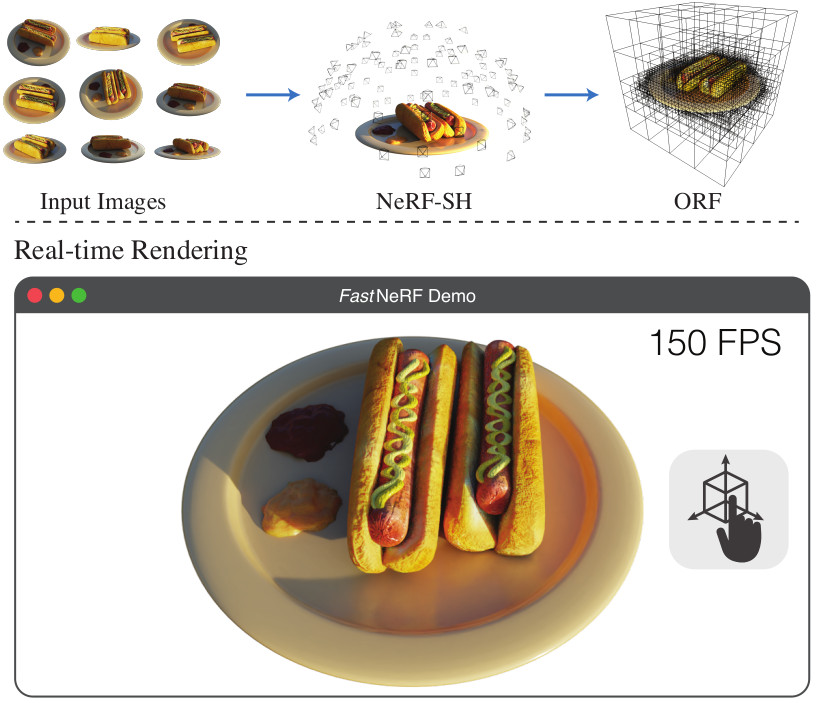
PlenOctrees for Real-time Rendering of Neural Radiance Fields
We introduce a method to render Neural Radiance Fields (NeRFs) in real time using PlenOctrees, an octree-based 3D representation which supports view-dependent effects. Our method can render 800x800 images at more than 150 FPS, which is over 3000 times faster than conventional NeRFs. We do so without sacrificing quality while preserving the ability of NeRFs to perform free-viewpoint rendering of scenes with arbitrary geometry and view-dependent effects. Real-time performance is achieved by pre-tabulating the NeRF into a PlenOctree. In order to preserve view-dependent effects such as specularities, we factorize the appearance via closed-form spherical basis functions. Specifically, we show that it is possible to train NeRFs to predict a spherical harmonic representation of radiance, removing the viewing direction as an input to the neural network. Furthermore, we show that PlenOctrees can be directly optimized to further minimize the reconstruction loss, which leads to equal or better quality compared to competing methods. Moreover, this octree optimization step can be used to reduce the training time, as we no longer need to wait for the NeRF training to converge fully. Our real-time neural rendering approach may potentially enable new applications such as 6-DOF industrial and product visualizations, as well as next generation AR/VR systems. PlenOctrees are amenable to in-browser rendering as well; please visit the project page for the interactive online demo.
pixelNeRF: Neural Radiance Fields from One or Few Images
We propose pixelNeRF, a learning framework that predicts a continuous neural scene representation conditioned on one or few input images. The existing approach for constructing neural radiance fields involves optimizing the representation to every scene independently, requiring many calibrated views and significant compute time. We take a step towards resolving these shortcomings by introducing an architecture that conditions a NeRF on image inputs in a fully convolutional manner. This allows the network to be trained across multiple scenes to learn a scene prior, enabling it to perform novel view synthesis in a feed-forward manner from a sparse set of views (as few as one).
The Breakthrough Listen Search for Intelligent Life: Data Formats, Reduction and Archiving
Breakthrough Listen is the most comprehensive and sensitive search for extraterrestrial intelligence (SETI) to date, employing a collection of international observational facilities including both radio and optical telescopes. During the first three years of the Listen program, thousands of targets have been observed with the Green Bank Telescope (GBT), Parkes Telescope and Automated Planet Finder. At GBT and Parkes, observations have been performed ranging from 700 MHz to 26 GHz, with raw data volumes averaging over 1PB / day... In this paper, we describe the hardware and software pipeline used for collection, reduction, archival, and public dissemination of Listen data.